|
Determining when process variables are in steady state is intuitively a simple task. Creating a MATLAB agent to perform this operation in a reliable and robust manner, however, is not trivial -- especially in the presence of noise. We have adopted a scheme that, like the Dynamic Data Reconcilation Agent, processes the previous H samples of the data stream; we then use linear regression to determine m = the slope of the line that fits the data with minimum mean square error and compare the magnitude of that slope with a threshold; when |m| is less than the threshold for D successive samples the variable is declared to be in steady state. The parameters H and D are for tuning; clearly they will need to be adjusted depending on the noise levels and process variables' dynamic behaviour (effective time constants). These factors are readily determined by observing the signals, so the SSTD agent was designed to adapt accordingly. With multiple variables steady state is only declared when all of them have met the corresponding conditions. A demonstration of the behaviour of the SSTD agent's performance is shown in Figure 1. The steady-state (SS) flag switches to unity when the variable settles to steady state and reverts to zero when a transient occurs. (The SS Flag plots below are scaled to permit plotting with the corresponding process variables.) Observe that the linear regression slope is quite noisy for the H chosen (H = 30) -- this illustrates that tuning H and D is quite important, and that the declaration of steady state may be quite conservative in such cases. 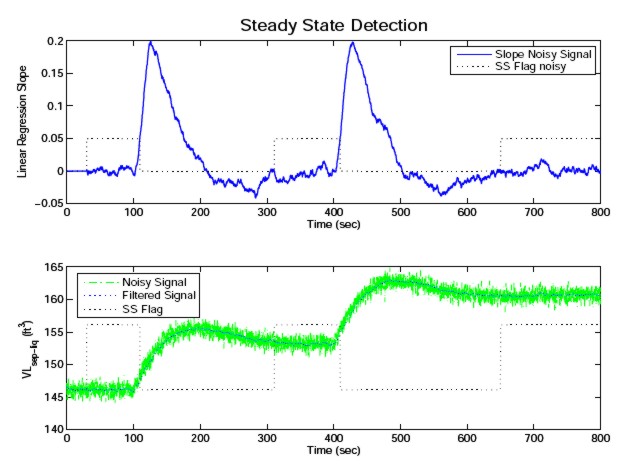 Figure 1. Demonstration of Steady-state/Transient Determination The design and implementation of the SSTD Agent is a part of Pilar Moreno's Masters research; it will be described in more detail in her thesis (to be defended and published in January 2010) and a conference paper to be submitted at that time. This part of the UNB PAWS effort has been completed and delivered. Return to the UNB PAWS Home Page Information supplied by: Jim Taylor Last update: 9 December 2009 Email requests for further information to: Jim Taylor (jtaylor@unb.ca) |