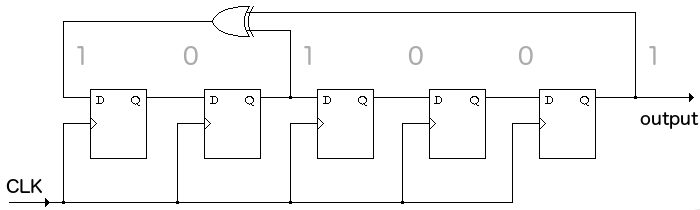
This linear feedback circuit produces an output bit stream with a random appearance
and a period 31 bits long, as 1010111011000111110011010010000....
A random sequence of bits (ones/zeros) should statistically resemble a sequence of coin tosses (heads/tails) where the independent probability of the next bit in the sequence being 1 or 0 equals 0.5 and other properties follow. The sequence of bits produced by a linear feedback digital circuit cannot be truly random because the sequence of states is deterministic (predictable) and a shift register with N flip flops can only take on 2N different states. Consequently, although bit sequences produced in this way may appear random, they are necessarily periodic and for that reason are called pseudo-random number sequences or PN-sequences and the circuit is called a pseudo random number generator (PRNG). In practice, a PN-sequence is also a maximum length sequence or m-sequence for a given shift register configuration.

This linear feedback circuit produces an output bit stream with a random appearance
and a period 31 bits long, as 1010111011000111110011010010000....
The ideal pseudo random number generator will produce the longest possible period before repeating. Note that if the state of the above circuit becomes all zeros it will never change, so this condition must be avoided. Therefore, the maximum length sequence is given by L = 2N-1, where N is the number of flip flops. In the above circuit with five flip flops, the maximum length sequence with a 31-bit period has been obtained.
A maximum length sequence has the statistical properties expected of random bits, such as "an equal number of 1's and 0's", which is almost true, but not exactly possible with the odd number of bits L = 2N-1. The above sequence has 16 ones and 15 zeros. This difference is less important for very long periods.
In general, the feedback loop connects the shift register output back to the input and optionally a XOR gate connection (tap) or not at each internal flip flop of the shift register. In this example, only one flip-flop output feeds an XOR gate while the others are not connected, as shown labelled (101001) corresponding to the polynomial:
P(x) = x5 + x3 + 1
In this way the polynomial P(x) defines the circuit and the specific sequence of states depends only on P(x) and the starting value of the circuit.
If a polynomial P(x) of degree N gives a maximum length sequence, the length will be L = 2N-1.
Use of an irreducible polynomial P(x) is a necessary but not sufficient condition for a maximum length sequence. The polynomial P(x) must also be primitive.
Conversely, is possible to define a primitive polynomial as being a P(x) that gives a maximum length sequence.
It follows that the above polynomial P(x) = x5 + x3 + 1 is primitive. For this polynomial of degree 5, let M=25-1=31 and it can be shown that P(x) is a factor of x31+1 but no smaller M.
Question: What polynomials would give a maximum length sequence of L=31?
Answer: Only primitive polynomials of degree 5 will give length L = 25-1 = 31.
The prime factors of x31+1 are: (check)
Only these six prime factors of degree 5 could give PRNG sequences of length 31. They must each be checked to be certain they do not factor a smaller xL+1. In this case, all six polynomials are primitive and any of them would lead to a maximum length sequence.
Finally, note the symmetry between pairs of these six results; there are three pairs of polynomials which are mirror images of each other. This is a property of irreducible polynomials.
![]() See all prime polynomials from 0..511
See all prime polynomials from 0..511
![]() Online
Linear Recursive Sequence Tool
Online
Linear Recursive Sequence Tool